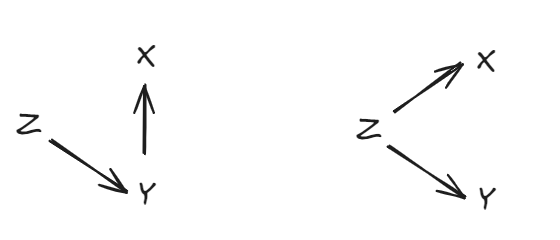In the literature I have often seen conflicting definitions for terms like “transfer learning” and “meta learning”. E.g. here’s a stackexchange question about this.

Here’s the general framework encapsulating this idea.

Suppose our universe of interest is given by some joint distribution \(P(\textbf{X})\). This joint distribution is itself not known to us (we want to learn it, after all) but instead we have some distribution \(\phi_{p_{\mathbf{X}}}\) on the space of possible models. Specific tasks of interest to us like \(P(X_1)\), \(P(Y_2\mid X_1)\) etc. are derived as marginals of the joint distribution, and therefore are “random variables” derived from \(\phi_{p_{\mathbf{X}}}\) which may be correlated etc.

(Note how this is different from the usual “learning from data” setting in which we have a “prior” \(P(\mathbf{X})\) which we condition on observed data. In this usual setting, \(\mathbf{X}\) is a random vector including random variables for observations \(X_1,X_2,\dots\) and we can simply calculate the conditionals \(P(\mathbf{X}\mid X_1=x_1,X_2=x_2)\).)

One way to think about this is to say there’s some other (not included in \(\mathbf{X}\)) random variable \(Z\) such that \(P(\mathbf{X})\) depends on \(Z\), i.e. \(P(\mathbf{X}\mid Z)\) is a thing, and is what you know. Then when you “learn” the marginal \(P(X_1)\), you are also getting information on \(Z\), which gives you information on other distributions like \(P(X_2)\) or \(P(Y_2\mid X_1)\), which are also marginalized on \(Z\).

Meta-learning / generalization

Meta-learning in a general sense refers to learning this meta-distribution \(\phi_{p_\mathbf{X}}\) from data. What this means is we now see \(\phi_{p_\mathbf{X}}\) as a distribution that can be sampled from, not just a belief distribution — i.e. we see \(Z\) as a random variable that can be sampled.

In the classic meta-learning example of learning random sinusoids (see e.g.): the \(\phi_{p_{\mathbf{X}}}\) to be learned assigns high probabilities only to sinusoidal \(P(Y\mid X)\)s — equivalently \(Z\) is a random variable representing the generative model, and \(P(Y\mid Z,X)\) is known to be straightforward functional application so \(Y=Z(X)\).

Example: General transfer learning.

Here, learning \(P(Y_1\mid X_1)\) helps you learn \(P(Y_2\mid X_2)\).

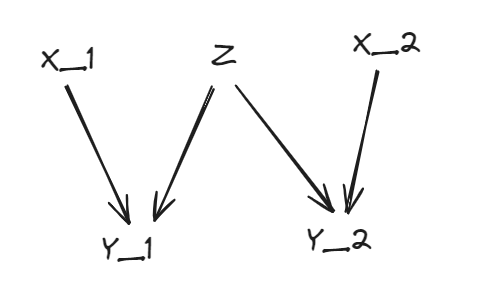
Note that this doesn’t mean \(P(Y_1\mid X_1)\) and \(P(Y_2\mid X_2)\) are the same or similar in any way (this can be taken as the special case where \(Z\) is simply exactly a distribution \(P(Y\mid X)\) and \(Y_i\) is (i.e. \(P(Y_i\mid X_i,Z)\) is such that:) is just composition \(Z(X_i)\)) — as is the case with most standard transfer learning applications such as fine-tuning and style transfer.

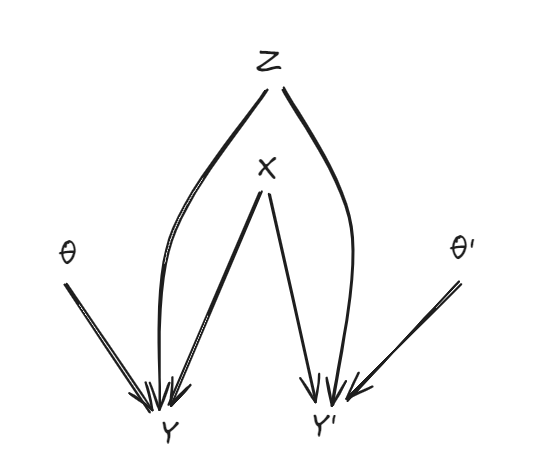
Style transfer looks like — \(\theta\) and \(\theta’\) represent two different “styles” (e.g. “formal voice” and “pirate voice”) and \(Z\) represents exactly some common distribution \(P(Y\mid X,\theta)=P(Y’\mid X,\theta’)\) so that the functional dependence of \(Y\) and \(Y’\) on their inputs \(X\) is completely determined by it.

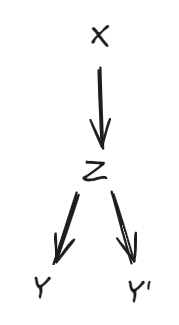
In fine-tuning, the correlation between \(P(Y\mid X)\) and \(P(Y’\mid X)\) is governed by a mediating variable — a latent.

Example: Semi-supervised learning.

Semi-supervised learning is possible when there \(P(X)\) and \(P(Y\mid X)\) are correlated as random variables when sampled from \(\phi_{p_\mathbf{X}}\). \(\newcommand{\corr}{\not\!\perp\!\!\!\perp}\)

Equivalently, if there is a random variable \(Z\) such that \(P(X)\) and \(P(Y\mid X)\) both depend on it, i.e. \(X\corr Z\) and \(Y\corr Z\mid X\) (where \(\corr\) indicates mutual information and \(a\corr b\mid c\) indicates conditional mutual information).

I’ve written about this with more exposition here, but this is only possible if \(X\) and \(Y\) have a common cause \(Z\) or if \(Y\) causes \(X\) (in which case you could simply let \(Z\) be \(Y\)). Semi-supervised learning is not possible when the only causal relationship between \(X\) and \(Y\) is \(X\to Y\) — this is known as the principle of independent causal mechanisms.