Information theory of multiple random variables

In the previous articles [1] [2] we defined the information of an observation as the logarithm of its probability – and its entropy of a random variable as the expected amount of information gained from observing it (and thus is a measure of how little information the prior carries). Naturally in the multivariate case it is trivial to define a “joint information” that is the logarithm of the joint distribution. and we have the joint entropy:

\[H(\mathbf{X})=-\sum_{\mathbf{x}}{p(\mathbf{x})\log p(\mathbf{x})}\]

Because the full joint distribution is at least as informative as the marginal distributions taken separately, we have the property:

\[H(X,Y)\le H(X)+H(Y)\]

We often informally explain notions of independence and relationships between random variables in terms of information – with information theory, we can now formalize these descriptions. The Venn diagram below shows the additive relationships between various entropies of multiple random variables:

#+ATTR_HTML: :width 400

(source)

$H(X)$ and $H(Y)$ are represented by the respective circles, $H(X,Y)$ is represented by the combined area of the circles and the mutual entropy; conditional entropies are as indicated. The mutual entropy (more commonly mutual information) is the expectation of the mutual information (more commonly pointwise mutual information):

\[\operatorname{pmi}(x;y) \equiv \log\frac{p(x,y)}{p(x)p(y)} = \log\frac{p(x|y)}{p(x)} = \log\frac{p(y|x)}{p(y)}\]

Even though the pointwise mutual information may be positive or negative (the probability of $y$ may go up or down depending on the observed $x$), its expectation is always positive in a way analogous to conservation of expected evidence. These ideas can be generalized to beyond two variables:

#+ATTR_HTML: :width 400

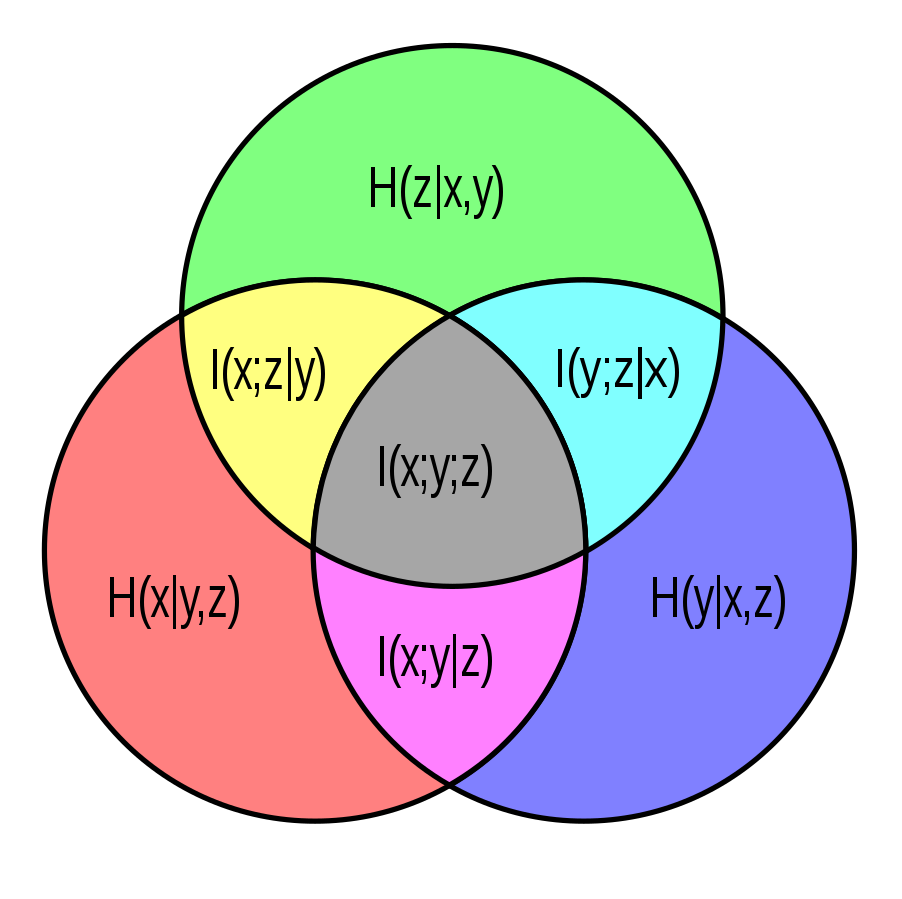(source)

The mutual entropy represents the reduction in the number of bits necessary to encode two correlated variables together, as opposed to separately. This is a special example of the entropy gain (or “Kullback-Leibler divergence”) of two probability distributions $p$ and $q$: it is the expected number of extra bits used when expressing a $p(x)$-distributed random variable with a $q(x)$-entropy encoding. The mutual entropy is the entropy gain from $f_{X,Y}(x,y)$ of $f_X(x)f_Y(y)$.

\[\begin{align*}KL(p(X) | q(X)) &= \sum-p(x) \log {q(x)} - \sum -p(x) \log {p(x)} \\&= \sum p(x) \log \frac{p(x)}{q(x)}\end{align*}\]

The first term of this expression (the number of bits required to express the random variable in the incorrect encoding) is also known as the cross-entropy.